Short notes and Formulas for Mensuration (2D figures)

In this article, we have discussed formulas of important 2D figures which are frequently asked. We have compiled important information which are mostly asked in SSC Exams at one place.

# Rectangle

Let d1 and d2 are diagonals of the given rectangle ABCD.

then, both diagonals are equal but not perpendicular to each other.

 Area of rectangle = length x breadth and perimeter = 2(length+breadth)

# Path outside the rectangle

Suppose there is a park having length l and breadth b. There is a road of width x outside of it.

Then, Area of path = 2x (l + b + 2x)

# Path inside the rectangle

Suppose there is a park having length l and breadth b. There is a road of width x inside of it.

Then, Area of path = 2x (l + b – 2x)

# When there is a road along both the length and breadth of the park.

Then, Remaining area of Rectangle (shaded region) = (l–x) (b-x)
Area of the path = lx + bx – x2

# Circle: Given a circle of radius ‘r’

We recommend you learn this table as it will save your time in calculating these all.

If radius is ‘r’, then perimeter = 2πr and Area = πr2

Radius	Perimeter (2πr)	Area (πr2)
7	44	154
14	88	616
21	132	1386
28	176	2464
35	220	3850
42	264	5544

# Length of Rope
Let ‘d’ is the diameter of pulley and ‘r’ is the radius, then d = 2r. All pulleys are similar.

Length of rope = 2d + 2pr

 

Length of rope = 3d + 2pr

Length of rope = 4d + 2pr

Note: Trick to remember these formulas: number of pulleys x diameter + Perimeter of one pulley

#Sector

In this circle, ‘r’ is the radius, θ is the angle made by the arc of length ‘l’

Length of arc  Area of sector  Area of sector when ‘l’ is given

# Segment

Area of minor segment 

Area of major segment 

# Area of shaded portion

# Inradius and Circumradius of Square:

There is a square of side ‘a’; ‘r’ is the inradius and ‘R’ is the circumradius.

# Triangle:

Let ABC is a triangle and M1, M2 and M3 are medians of the given triangle.

Then, 

# Inradius of triangle:

Given, ABC is a triangle and a, b and c are the sides of given triangle. Let ‘r’ is the inradius of triangle.

 

# Circumradius of triangle:

Given, ABC is a triangle and a, b and c are the sides of given triangle. Let ‘R’ is the circumradius of triangle.

# Right angle triangle

Given ‘a’ is the base, ‘b’ is the perpendicular and ‘c’ is the hypotenuse of triangle ABC.

# Equilateral triangle:

 

 

Where, h is the height of triangle, 

Hence, we can say that height of equilateral triangle is equal to the sum of side perpendicular of the triangle.

# Isosceles triangle

# Regular Polygon

Let, n = no. of sides of regular polygon and a = length of side of regular polygon

# Internal angle of regular polygon = 

# Sum of internal angle of regular polygon  

# Angle made by centre = 

#Area of Regular polygon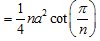 

 or  

# External angle of regular polygon 
# sum of all external angle = 360º

# For Regular Hexagon

Circumradius R = a Inradius

# Cyclic Quadrilateral

# Parallelogram

Let a and b are the sides, h is the height and d1 and d2 are the diagonals of parallelogram

then, 

Area of parallelogram = (i) Base × height

(ii) 

(iii) 

Imp. Relation 

Imp. Note: In rectangle, parallelogram, square and Rhombus diagonals bisect other.

# Rhombus

In Rhombus, diagonals are not equal to each other but they bisect each other at 90 degree. 

Area = Base × height = a x h

Or Area 

# Trapezium

Case 1: If AD = BC, then DM = CN

# Quadrilateral