
Quadratic equations – These are the equations which look like
ax2 + bx + c = 0
These equations are asked in the competitive examinations in a set of 5 questions. Enough with the theory, the question in exams look like -
In each of the following questions, two equations are given. Solve these equations and give answer:
A) If x >= y, i.e. x is greater than or equal to y
B) If x > y, i.e. x is greater than y
C) If x <= y, i.e. x is less than or equal to y
D) If x < y, i.e. x less than y
E) If x = y, or no relation can be established between x and y
Question 1:
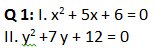 .
.Here we will discuss a method to solve these equations with minimal writing and as reduced time as possible. Keep in mind; we are doing exactly what we used to do before, just in a less time and less writing.

+b +c * +a Note that I have written coefficients along with their signs
+5 +6 * +1 Now, the next task for us is to find the factors in a way which when multiplied give c*a
+5 +6 (which is 6 in this case) and their sum or subtraction results b (5 in this case).
Now, the next task for us is to find the factors in a way which when multiplied give c*a (which is 6 in this case) and their sum or subtraction results b (5 in this case).
A way to find the factors
Start dividing the number formed using “c*a” starting from first prime number i.e. 2. The result gives one factor and the other factor is the number you divided with.Add them and then subtract them to see if they give “b”.
If not divide it with next number on number line i.e. 3 and so on till you get the final factors.
Don’t worry this method seems lengthy but with a little bit of practice it will get faster.
We have our factors 3 and 2 and now is the time to decide the sign. For that, riddle me this
3 + 1 = 4
3 + (-1) = 2
(-3) + 1 = -2
(-3) + (-1) = -4
Therefore, the factors become
 +3 +2
+3 +2
Isn’t this correct? Now, if we observe this, the sign of the result is similar to the sign of the bigger number in the calculation.
In the question above, we have the factors 3 and 2 and the result is required to be 5. The sign of the result (in this case 5) is + and therefore, the sign of bigger number (in this case 3) will be +.Now, as the sign of 3 is + and the required result is 5, the sign for 2 must also be +.
Remember two things before marking them as final answers:
1. Change the sign of the factors i.e. – if they are + and + if they are -.2. Divide the two factors by “a”.
In the above question, the value of “a” is 1. Therefore, the factors become


And for the last touch, we change the sign. After that we get the final factors.
Final factors
-3 -2
Don’t worry! It’s not that hard.
Let’s take one more example to make process more familiar to you.
x2 – 3x – 10
To find the factors, we start with dividing 10 by 2, we get 5. Therefore, the factors are 2 and 5. We need either the sum or the subtraction of the two to be 3, and (5-2) gives 3 which makes them the final factors.-3 -10*+1-3 -10
2 5
As for the sign, the sign of 3 is -, and therefore, the sign of bigger number (in this case 5) will be -.
2 -5
Let us check if this satisfies all the conditions
2 + (-5) = -3
2 * (-5) = -10
Yes it does and we have the factors.
For the last touch, we change the signs and divide them with “a”, which in this case is 1.
-2 5 The final factors

Hopefully, the method was crystal clear to you and comparatively easy then the traditional method. Let’s now take a question similar to the one asked in examination.
In each of the following questions two equations are given. Solve these equations and give answer:
A) If x >= y, i.e. x is greater than or equal to y
B) If x > y, i.e. x is greater than y
C) If x <= y, i.e. x is less than or equal to y
D) If x < y, i.e. x less than y
E) If x = y, or no relation can be established between x and y
Question 2:
I. x2 + 6x + 9 = 0II. 2y2 +3y - 5 = 0
x2 + 6x + 9 = 0
To find the factors, we start with dividing 9 by 2, which gives a fractional result and that is not acceptable. So, we divide 9 by 3 which gives 3. Now, we check for the sum or subtraction to be 6 with the two factors 3 and 3.+6 +9
3 3
As for the signs, we check with both the factors having + signs.
3 + 3 = 6
3 * 3 = 9
And we get our factors.
For the two unforgettable things to do i.e. division by “a” (1 in this case) and change of signs.
-3 -3 Values of x
For equation no. 2
2y2 +3y - 5 = 0
To find the factors, we start with dividing 10 by 2, we get 5. Therefore, the factors are 2 and 5. We need either the sum or the subtraction of the two to be 3, and (5-2) gives 3 which makes them the final factors.
+3 -5*+2+3 -10

As for the sign, the sign of 3 is +, and therefore, the sign of bigger number (in this case 5) will be + and (5 – 2) = 3. Therefore, the sign of 2 will be -.
5 2
5 -2Let us check if this satisfies all the conditions 5 + (-2) = 3
5 * (-2) = -10
Just a last tiny step, division by “a” (2 in this case) and change of sign.
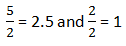
-2.5 1 Values of y
And we are ready for comparison.
Though I am always in favor of as minimum writing in examinations as possible, this time I recommend you write all the conclusions of comparisons to make your answer more accurate.
We compare every value of x to every value of y and note the results down.
| Value of x | Value of y | Conclusion |
|---|---|---|
| -3 (1st value) | -2.5 | x < y |
| -3 (1st value) | 1 | x < y |
| -3 (2nd value) | -2.5 | x < y |
| -3 (2nd value) | 1 | x < y |
Try practising a couple more equations because this constitutes a very important question in the examinations and comes in the set of 5 thus securing a chunk of marks. Hope this trick helps you.
Few practice problems
In each of the following questions two equations are given. Solve these equations and give answer:A) If x >= y, i.e. x is greater than or equal to y
B) If x > y, i.e. x is greater than y
C) If x <= y, i.e. x is less than or equal to y
D) If x < y, i.e. x less than y
E) If x = y, or no relation can be established between x and y

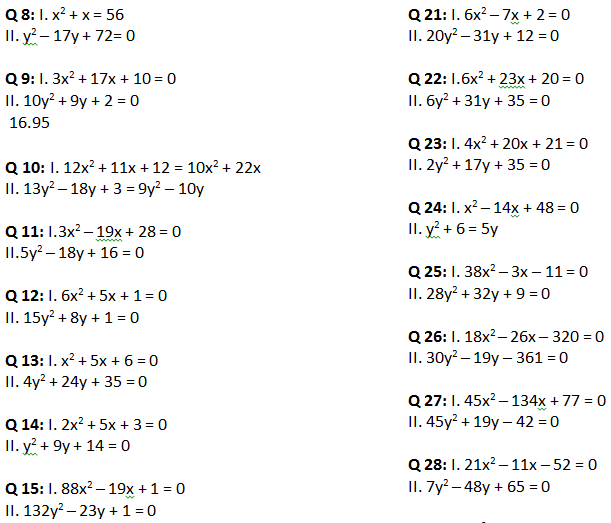

If there is a problem with any of the equation above, feel free to comment and we will try and solve it as soon as we can.
Comments
Post a Comment